Natural Shapes and Shadows
tl;dr: I made lamps about trees and ripples:

Shoulders. (Click to expand.)
A few years ago, through my academic work on park access and my project to cut mountains from paper, I got interested in using natural patterns to make soothing objects. Frederick Law Olmsted, the designer of Central Park in New York and Jackson Park in Chicago, described the influence of nature beautifully, in 1865:
the enjoyment of scenery employs the mind without fatigue and yet exercises it, tranquilizes it and yet enlivens it; and thus, through the influence of the mind over the body, gives the effect of refreshing rest and reinvigoration to the whole system.
More recently, E. O. Wilson’s Biophilia set the stage for biophilic design, though I was personally drawn to simulate not just living forms but natural phenomena more broadly.
It is at once inspiring and a little exasperating how academic work can rigorously (and ad nauseum) validate what we already “know,” or believe. The restorative psychological (executive function, etc.) and physiological (heart rate, cortisol) influence of exposures to nature have been measured rigorously (e.g., 1, 2). Parks and open spaces yield further health benefits as a venue for exercise and by fostering communities. Marc Berman’s lab at UChicago has measured how people process and respond to the visual cues of natural forms, and described the ways in which these forms are incorporated in architecture. These include self-similar patterns (fractals), multiple scales, semantic cues (ideas and words), colors, and so forth. The idea of delineating and quantifying the influences of nature that we all experience affected me strongly.
In short: I set out to use light to express the subtle curves of tree branches, and to echo the calm of ripples on a pond.
Modeling Natural Processes
I began by modeling processes and patterns. Algebra and computation offer two divergent paths for doing this. We can derive the solutions to mathematical equations for things like ripples in a coffee cup, vibrations on a drum, or waves in water. Or we can define the algorithms or “rules” for phenomena like the leaves or branches of trees, whose stochastic realizations are unique but intelligible.
Ripples and Waves
Just as sculptors study anatomy, I began by reviewing the physics. Science helps focus observations; the Feynman Lectures (47-51) are wonderful for this. How deep is the water? Are the ripples caused by gravity or by surface tension? How does a single crest move with respect to a group (group vs phase velocities)? The individual crests may move forward or backwards within a group, and different physics dominates at different scales.
Still, when I began to simulate the full lagoon, I was unsatisfied with my results. I may revisit this later: lots of people have figured it out. Just look at the animation of water in Moana or the video game Uncharted. But this presentation chronicles the years of work it took, to render the (dynamic, shaded) water of a single scene! Too much for my hobby project!
Solutions to the Laplace Equation on an Arbitrary Surface
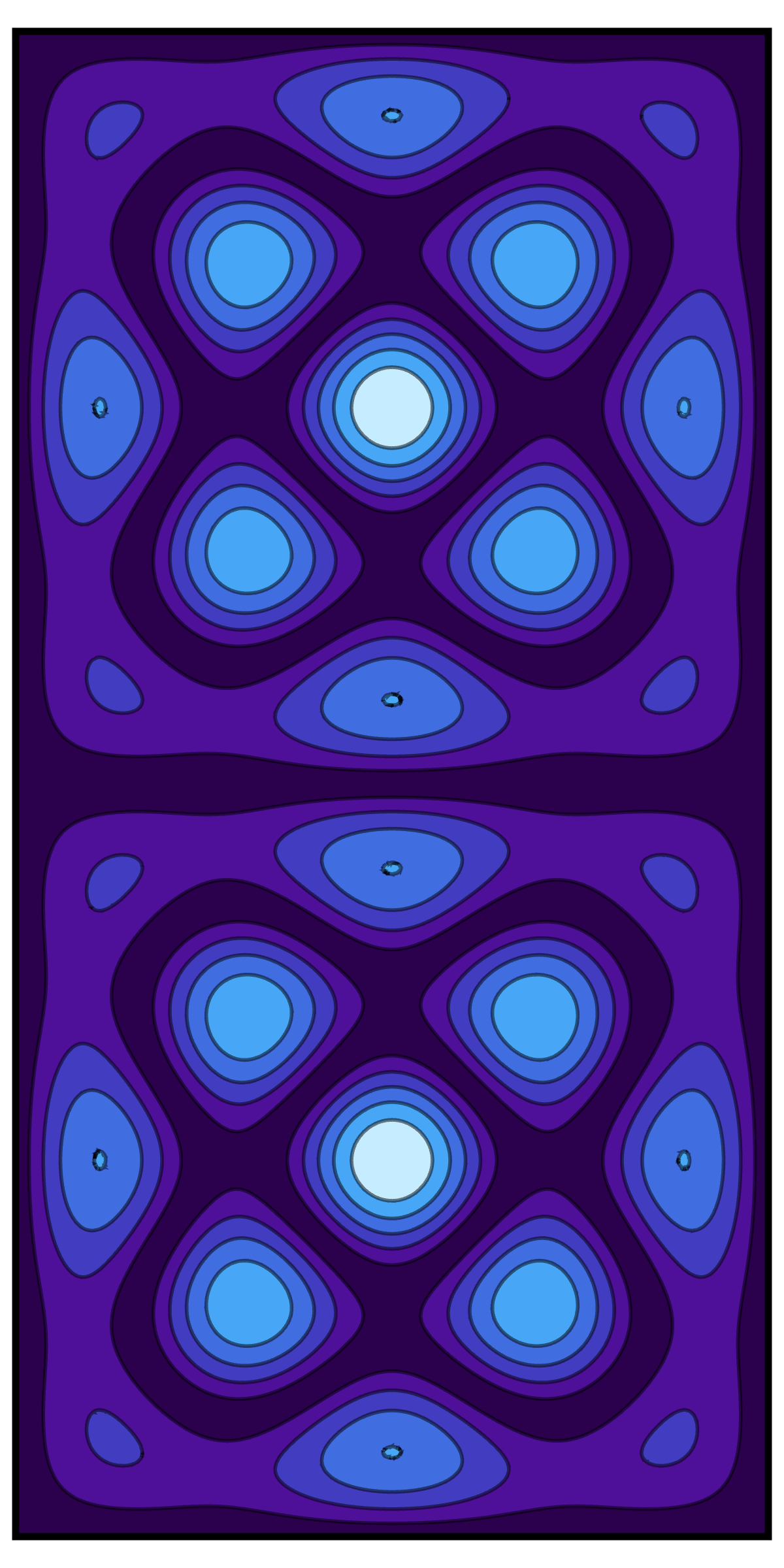
Failing to capture mathematically what I saw in the park, I fell back on one of the more enjoyable things that I learned from physics: the harmonic “ripples” of a membrane clamped along a boundary – a drum. These “harmonics” are the ways that your drum likes to shake, just like the fundamental of a piano string and its overtones. Or you and your dance playlist. If you’ve known me for a bit, I have probably raved at you about Bessel functions while banging on the table and scrutinizing the ripples in my coffee.1
You can solve this equation (the Laplace equation with Dirichlet boundary conditions) for any surface or shape, like so:2
ℒ = Laplacian[u[x, y], {x, y}];
ℬ = DirichletCondition[u[x, y] == 0., True];
poly = Rectangle[{0, 0}, {1, 2}];
{vals, funs} = NDEigensystem[{ℒ, ℬ, u[x, y], {x, y} ∈ poly, 100];
Without thinking too carefully, I played with a bunch of shapes in Mathematica, and found solutions that I liked for a 1×2 rectangle:
These have regular but non-trivial curves that feel a bit art nouveau. Now, if you’ve taken freshman physics, you may think that I have made a mistake with my math! The solutions to wave equations for rectangular surfaces are separable horizontally and vertically: sine waves each way! That means: a rectangular grid of ups and downs. We should find nothing so interesting! Nothing really, to “employ the mind without fatigue,” or “enliven it” at all!
The trick is that for rectangles like mine, where the horizontal and vertical directions are multiples of each other, you get “degenerate” solutions. Formally, this just means that the vibrating energy of the “drum” is equal for two of the boring configurations. For instance, 1 ripple up and 3 across, has equal energy on a square drum, to 3 up and 1 across. When that is true, you can replace solutions A and B with A + B and A − B, or indeed any “random” linear combination of A and B!3 As it happens, those “random” solutions are what Mathematica gave me, and I first chose “degenerate” solutions purely on aesthetic grounds. Only later did I wonder why I had gotten any interesting solutions, stop to think about the math, and select the “random” solution that I liked best.4 You can read about it more this in this paper, or find nice visualizations here.
Leaf Venation
As for venation patterns, the classic (and very readable) paper seems to be Modeling and visualization of leaf venation patterns by Runions et al. This straightforward, biologically-inspired algorithm yields excellent results, out of the box. The algorithm is initialized with
- A starting point, i.e. a stem.
- A set of destinations, distributed across an area, i.e. a leaf. Biologically, the destinations are sources of auxin, which attract growth.
It then loops on:
- Associate the auxin sources with the closest point on the existing veins.
- The existing veins are extended towards the set of sources for which they are the closest.
- Remove auxin sources that are close enough to an existing vein.
This algorithm has been coded, described, and applied with beautiful results by Jason Webb and by Nervous System, who in fact used it to make exquisite lamps and fonts (as well as an explanatory video).
As for me, I just made an M-leaf for my son, Morgan. My (very-rough) code is in this gist.

Venation pattern for an M, generated using the algorithm by Runions et al. (Click to expand.)
Though this did not fit my immediate aesthetic aims, the basic algorithm is clearly capable of very nice results. I look forward to revisiting this for generative grillwork/lattices.
Capturing Natural Processes
As a counterpoint to my mathematical toys, I set about taking pictures of trees and water. The challenge was that I needed to be able to laser cut my images!
Old-School Printing Techniques
My initial strategy for this was to write code to translate raster pictures into vector formats that were guaranteed to be fully-connected: lithographies/wood-cuts and hexagonal half-tones. This means using the brightness of the image to specify the width of cuts or the areas of hexagons, and determine how much light to let through a piece of wood. I found after the fact that the laser-cut half-tone process has been done before, most notably by Eric Forman. Here are some ripples from the Fox River and the Jackson Park Lagoon, as images, half-tone hexagons, and “lithographies”:
In principle this works pretty well, but in practice it requires large, contrasty images. One improves the fidelity of the representation by increasing the number of lines or hexagons, but the material, wood, sets an upper limit on this number. The half-tone process did yield evocative results – your eye can “graze” over the hexagon patterns much as you track the crest of a single ripple in a pool or seek the sharpest bend in a smoothly arcing tree branch. But I wanted viewers to understand consciously that they were looking at water, and my results were too abstract for this. This was all the more true with the “lithographies.”
Picturing Man and Nature
Next, I set out to capture silhouetted images that I could threshold directly. In other words: take pictures of shadows, and convert those into laser-cut designs. Photographing and processing a scene into a “legible” silhouette is harder than I first supposed. It took me many months to get just a few acceptable images. Here are trees set against trusses, natural against manmade forms:
The similarities are clear: thicker load-bearing masts and the increasingly delicate branches and “twigs.” Both exhibit fractal patterns that follow from shared structural requirements. But while the components of the bridge are straight and regular and the “limbs” are supported from multiple points, trees’ branches curve and fork without loops. However, since any weight must be supported, the shadows are all connected and lend themselves to laser cutting.
Creating Light and Shadow
Finally, I processed the images and wrote code to format them for the laser cutter. I cut the trees and bridges, backed them with linen paper to diffuse the light, and designed a “box” to hold them.


















Shoulders: Norfolk Southern rail bridge over the Calumet River, Jackson Park Chicago, and the Saginaw Forest.
Laser-cut wood panels backed with linen paper.
I called this lamp “Shoulders,” because it’s mostly images of Chicago, and because they are bearing loads.
Of course, once we have a box, we can “trivially” assemble different ideas: time and length scales, cycles, natural vs designed, etc. For example, this lamp sets two pictures of ripples against two of the harmonics for the 1 × 2 surface from above. This grouping counterposes not man and nature but analytical solutions to physical equations against the phenomena as we observe them in the world. Universal laws vs ephermeral realities, if you will:


Ripples: thresholded images of the Jackson Park Lagoon, with solutions to the Laplace equation for a 1 × 2 surface.
Yet again, perhaps more prosaic, I spent literally a year taking shadow pictures of leaves through the four seasons:


Seaons: trees in Jackson park, through the year.
Happy Fall!
Notes:
-
This is probably my favorite basic “factoid” from physics, though the resonant depolarization of the electron beam at LEP, used to get the mass of the Z boson, is a close second. Ask me about it for bonus ravings! ↩
-
For this particular surface,
DEigensystemworks too, since it is algebraically solvable / trivial. ↩ -
For the eigensystem, the two solutions built from A and B must be mutually orthogonal. ↩
-
That is, I chose the angle of rotation for pairs of separable solutions. ↩